'In nature, Golden Ratio (Phi) and Fibonacci Numbers (FN) are common, probably reflecting the practicalities of life. In our human world, we might see them where they don't exist, but where they do, we find them pleasing. Whether we are attracted to them by the mystic of mathematics or the aesthetics they produce is uncertain.' ... Tim Entwise in Blueprint for Living
Watch a pleasant 2.5 minute presentation on the Golden Ratio here but do not believe everything that is said in the video.
Indeed, there is a lot of hype about Phi and FN - the golden ratio, also known as the golden section or golden mean, is claimed even to connect humans to God!! (It is claimed that in ɸ, He has crossed nothingness (0) by unity (1) to obtain the symbol for the golden ratio. But note that the symbol ɸ was adopted only recently for the golden ratio!). It is stated that 'The Golden Section, or Phi, found throughout nature, also applies in undertanding the relationship of God to Creation'.
Many attempts have been made to bring order to the situation regarding hypes and myths about Phi and FN. Please click here and here.
Phi is an amazing number with some unique mathematical properties and this is what we shall be looking at in this blog - the aim is to give some examples invoving Phi and FN that have a wow factor - that is what recreational maths is all about.
First, we define the golden ratio and Fibonacci Numbers: The golden ratio is denoted by the greek letter capital Phi ɸ and its inverse by lower case phi φ.
(Click on a slide to see full page image. Press ESC to return to Text)
Fibonacci Numbers are intimately related to the Golden Ratio and are claimed to occur widely in nature. I define them in the following slide - a more general and detailed discussion is available in my blog.
First, I would like to show how closely, Phi that is purely geometrical in origin is related to Fibonacci Numbers which are formed from numbers following a simple mathematical prescription.
The second term in the expression for Fn becomes progressively smaller as n increases, and to a very good approximation Fn increases as ɸ to the power n for n greater than about 10.
Also, notice that the second term is negative when n is even and positive for odd values of n. For small values of n, Fn oscillates about the values calculated for ɸ to the power n. This is explained in the next slide:
Puzzle 1: Climbing Steps: The puzzle may be stated as follows:
You would like to climb six steps. You can either climb one step at a time (s1) or two steps at a time (s2). How many differnt ways can you climb the steps?
One way to solve the problem is to work sequencially
First Step: - only one way -- 1s1; N1 = 1
Second Step: 2s1 or 1s2. N2 = 2
Third Step: 3s1; 1s1+1s2; 1s2+1s1. N3 = 3
Fourth Step: 4s1; 2s1+1s2; 1s2+ 2s1; 1s1+1s2+1s1; 2s2. N4 = 5
Fifth Step: 5s1; 3s1+1s2; 2s1+1s2+1s1; 1s1+2s2; 1s1+1s2+2s1; 2s2+1s1; 1s2+1s1+1s2; 1s2+3s1. N = 8 (6th Fibonacci number)
Sixth Step: 6s1; 4s1+1s2; 3s1+1s2+1s1; 2s1+2s2; 2s1+1s2+2s1; 1s1+2s2+1s1; 1s1+1s2+3s1; 1s1+1s2+1s1+1s2; 3s2; 2s2+2s1; 1s2+4s1; 1s2+2s1+1s2; 1s2+1s1+1s2+1s1. N = 13 (7th Fibinacci Number)
Notice the sequence of Fibonacci numbers 1, 2, 3, 5, 8, 13 appears here. It is now straightforward to calculate the number of different ways you can climb 10 steps. It is FN at n = 11 --- this is 144.
Puzzle 2: Seating Arrangement:
At a school function with lots of children (C) and adults (A), the seating arrangement requires that an adult (A) must not sit next to another adult. If there are N chairs then how many different ways they may be seated?
According to the puzzle, combinations AA are not allowed. Let us start with one chair
1 chair: C or A. N1 = 2
2 chairs: CC; CA; AC. N2 = 3
3 chairs: CCC; CCA; CAC; ACC; ACA. N3 = 5
4 chairs: CCCC; CCCA; CCAC; CACC, CACA; ACCC, ACCA; ACAC. N4 = 8
5 chairs: CCCCC; CCCCA; CCCAC; CCACC; CCACA; CACCC; CACCA; CACAC; ACCCC; ACCCA; ACCAC; ACACC, ACACA. N5 = 13
and so on...
Again the sequence of Fibonacci numbers 2, 3, 5, 8, 13,...appears. The number of different ways the visitors may be seated increases by ɸ = 1.618033 each time an extra chair is added.
An Example from Biology: Let us look at the family tree of bees. The situation may be stated as follows:
In a beehive, there is one female queen who lays all the eggs.
If an egg is fertilized by a male bee, then the egg hatches into a female bee.
But if the egg is not fertilized then it hatches into a male bee (a drone).
Worker female bees do not lay eggs.
Essentially, a drone has one parent while a female bee has two parents. We wish to map out a family tree for bees. I have prepared the next slide to show this:
Interestingly, FN and ɸ appear in the most unlikely places - before I discuss more examples, let us expand on the scope of the golden ratio that has been defined for a line (one-dimension) so far. Extend to two or three dimensions and we encounter some fascinating observations.
Golden Rectangle: The sides of a golden rectangle are in the ratio ɸ = 1.618033.
Claims have been made that the proportions (aspect ratio) of a golden rectangle are aesthetically most pleasing, and this is reflected in architectural designs; art; paintings; aspect ratio of books, cards and many other objects. I think it is fair to say that a proprtion around ɸ might be preferred by many but the popular range for aspect ratio b/a of objects is more like ɸ ± 20%. Similarly, claims about proprtion of human body parts etc. do not stand up to scrutiny.
However, an aspect ratio based around the golden ratio may have some truth. I shall stick my neck out here and say that when we look at the view in front of us, we see a larger horizontal span but the size of our vertical view is truncated by the ground we are standing on. This trains our mind to function best when we have a view that is about 1.5 times wider than it is higher - and it is possible that a preference of this kind of aspect ratio might be hard-wired in our aesthetics.
Fibonacci Spiral: Also referred to as a Golden Spiral and a source of untold confusion in popular science articles.
If you google 'spirals in nature and design', you will find a large collection of articles about discovering spiral patterns in nature and art with some very nice pictures too. Mostly it is the logarithmic spiral that one observes but in many publications it is claimed that what we are seeing is the golden spiral with every 90 degrees turn, the size of the spiral increases by the golden ratio (1.618033...). This generally does not stand up to scrutiny - for instance, a popular example is the size of the nautilus shell. The shell does grow as a logarithmic spiral but the growth per ninety degree turn is not the golden ratio (1.618033...) but has been measured to range from 1.33 ± 20% to 1.7.
I find the logarithmic spiral fascinating and shall discuss it in more detail here. First thing to note is that Fibonacci spiral has constant 'local' curvature (quarter circles in successive squares) while a logarithmic spiral (golden spiral is a special case of it) has a continuously varying curvature.
The next slides list some interesting properties and examples of logarithmic spirals:

Did you know that a peregrine falcon, while hunting, swoops at speeds up to 220 miles per hour (~360 km/hour) - fastest speed of any animal in the world!!
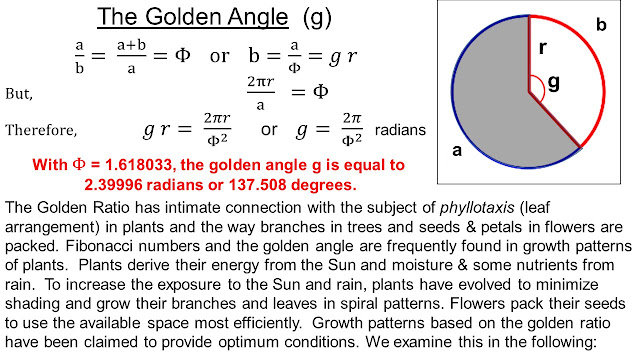
Golden Angle: If we divide the circumference of a circle in two parts according to Euclid's prescription (effectively, change the straight line to make the perimeter of a circle) then the smaller of the two angles is called the Golden Angle.
The question is: For a new primodium to start, the plant must know where the least crowded spot on the meristem is? The best location seems to be situated at an angle equal to the golden angle from the last primordium - but how does the plant know this? This is where it gets technical - A full description of phyllotaxis is not yet established and lot of questions remain. I shall give a very brief summary.
Molecular-genetic experiments indicate that active transport of the plant hormone auxin is the key process regulating phyllotaxis. Auxin is a plant hormone produced in the stem tip that promotes cell elongation. Organ primordia produce an inhibitory field - depleted local auxin levels - that prevents organ initiation within a certain proximity.
Mechanical stresses from cell deformation at the site of primordia are also hypothesized to play an important role.
Locating new primordia at exact separation of 137.5 degrees is not understood although some attempts have been made on the basis of packing seeds in a limited space.
Regular Pentagon and The Petagram: I discuss these as a pentagram has some unique mathematical properties and the sides and angles of a pentagram are intimately connected to the golden ratio. Because of its symmetry, a pentagram has been attractive to mathmaticians, designers etc.
Final Note: I have really enjoyed working on this blog article. The Golden Ratio is an amazing number and I only wish that people do not hype its relevance to nature and humans too much. It is a pure geometrical delight and its close relation to Fibonacci Numbers is a great surprise to me - that is why mathematics is so much fun - great feeling of wonder and very satisfying when you have completed a proof.
I am not finished with Phyllotaxis and hope to return to it sometime in future - first I need to find a friendly botanist in the University with some spare time!
By the way, you can look here to see how they even find Golden Ratio and Fibonacci Numbers in the stock market - almost as fantastic as our theology friends.
PS: The golden ratio springs up in unexpected places - a popular maths puzzle is 6ܑⁿ + 4ⁿ = 9ⁿ. The value of n is actually related to the inverse of the golden ratio. Amazing!
Pass the web link to your friends if you have enjoyed reading it.
Pass the web link to your friends if you have enjoyed reading it.



















No comments:
Post a Comment