skip to main |
skip to sidebar
Who am I? Index of Blogs
I recently came across a paper by Paul Yiu entitled 'Iterations of Sum of Powers of Digits'. I thought that it was a delightful play on numbers and after trying it out on my 13 years old grand-daughter, I decided that everybody can enjoy the quaint results (presented in a formal way in the paper).
I shall attempt to present the discussion in a more layman friendly jargon - enjoy!
See also the article in Wiki on Happy Numbers.
Starter: We shall try powers of 2 first - the idea is as follows:
Choose a number N,
Sum the square of digits in the number N to obtain S1
Sum the square of digits in S1 to obtain S2
Continue doing this ...
What do you get ??
Best to check it out - Let N = 239
Then S1 = 2^2 + 3^2 + 9^2 = 4 + 9 + 81 = 94
S2 = 9^2 + 4^2 = 81 + 16 = 97
S3 = 9^2 + 7^2 = 81 + 49 = 130
S4 = 1^2 + 3^2 + 0^2 = 1 + 9 +0 = 10
S5 = 1^2 + 0^2 = 1
Any further iterations will leave the sum at 1.
Digit one is a fixed Point.
If we start with any of following numbers, then we shall obtain the fixed point equal to 1.
1, 7, 10, 13, 19, 23, 28, 31, 32, 44, 49, 68, 70, 79, 82, 86, 97, 91, 100
These are also known as Happy Numbers.
The happiness of a number is unaffected by rearranging the digits, and by inserting or removing any number of zeros in the number.
Numbers in red are prime numbers and are called Happy Primes.
What about the remaining numbers - the so-called sad numbers.
Nothing better than trying it out. Let us choose N = 83
Then S1 = 8^2 + 3^2 = 64 + 9 = 73
S2 = 7^2 + 3^2 = 49 + 9 = 58
Likewise... S3 = 89, S4 = 145, S5 = 42, S6 = 20,
S7 = 4, S8 = 16, S9 = 37 and S10 = 58
Notice that S10 = 58 = S2.
This simply means that further iterations will repeat the sequence from S2 to S10 - indefinitely. Sad numbers are trapped in a cycle - let us call it a limit cycle.
For the sum of squares of the digits in a number,
the limit cycle is 58, 89, 145, 42, 20, 4, 16, 37, 58.
Where one enters the limit cycle depends on the starting number
(Click on the slide to view full page image, press Escape to return to text)
The fixed point 1 and the limit cycle are the only final outcomes of iterations of sum of squares of digits in any number!
Sum of Cubes: There are five fixed points and four limit cycles in this case. 85.5% end up in fixed points and only 14.5% end in limit cycles. They are best shown in the following slide:
An examples: Let us start with N = 275
Then S1 = 2^3 + 7^3 + 5^3 = 8 + 343 + 125 = 476
S2 = 64 + 343 + 216 =623
S3 = 216 + 8 + 27 = 351
S4 = 27 + 125 + 1 = 153
S5 = 1 + 125 + 27 = 153 A Fixed Point
See also where a short computer program is also provided to calculate the fixed points and limit cycles.
Sum of Fourth Powers: There are 4 fixed points and 2 limit cycles in this case. Vast majority of iterations ( ~ 79%) end up in a limit cycle with 7 nodes (shown in the slide below).
The fixed point 8208 occurs with overwhelming frequency (> 90%) relative to other fixed points.
Why do Fixed Points and Limit Cycles Happen?
I now wish to find out why we get fixed points and limit cycles.
Let us consider the example of a number that is made of 5 digits and consider that we are iterating with sum of each digit raised to the power 3.
The maximum possible sum of the cubes of digits in a 5 digit number (for N = 99999) is 5 x 9^3 = 3645
The smallest 5 digit number is 10,000 which is larger than 3645.
An iteration reduces the magnitude of the number.
This is true for any number that has 5 or more digits.
For a number with 4 digits,
the maximum possible sum of cube of digits is 4 x 9^3 = 2916.
Some 4-digit number (1,000 to 2915) are indeed less than 2916 and the value of a 4-digit number is not necessarily reduced after an iteration.
Therefore, a sum of cubes iteration on an arbitrarily large number (of 5 or more digits) will always result in a smaller number (the final theoretical maximum value of the sum being 2916) but not for a number with four or fewer digits.
The sum of cubes is a finite set of numbers, from 1 to 2916, and an iteration will eventually reproduce a value that is already achieved in a previous iteration - a limit cycle is formed.
Fixed points are special cases of a limit cycle with just one element or node.
Likewise, for sum of squares,
the theoretical maximum value of the sum is 3 x 9^2 = 243
It may be shown that for an n digit number N, if n > k + 1 where k is the power to which each digit is raised, N is always greater than the sum of kth power of digits. Fixed points and limit cycles will lie in the range from 1 to (k+1) x 9^k.
Sum of first Powers (Sum of digits): This is a special case and I have left its discussion to this last section.
Iterations of the sum of the digits in a number result in fixed points from 1 to 9.
Fixed Points: 1, 2, 3, 4, 5, 6, 7, 8 and 9
Let us consider the case of a five digit number N = abcde
This is
N = 10000 a + 1000 b + 100 c + 10 d + e
Sum of digits S1 is
S1 = a + b + c + d + e
N - S1 = 9999 a + 999 b + 99 c + 9 d
We notice that N - S1 is completely divisible by 9.
Essentially, the first iteration on N has reduced its value by an amount that is a multiple of 9.
Depending on the initial number of digits in N, S1 will have a much smaller number of digits let us say that
S1 = fgh or S1 = 100 f + 10 g + h
The next iteration will reduce S1 by a multiple of 9 and will, in general, leave a fixed point remainder.
Summing digits may be used to find the remainder (in the range from 1 to 8) when the number is divided by 9.
A remainder equal to 9 means that the original number is divisible by 9
Example: Consider a number N = 659824753
Sum of digits S1 = 49
Next iteration S2 = 13
Next iteration S3 = 4
If N is divided by 9 then the remainder will be 4
http://ektalks.blogspot.co.uk/2017/10/blogger-profile-about-me-my-name-is.html
Who am I? Index of Blogs
In fifty two years of driving, I have had five accidents. Four of these were somebody running into the back of my car at a traffic light or at a roundabout. My experience is supported by data that nearly 25% accidents are rear-end collisions and short separation between vehicles is the cause.
Why do we pack closely at traffic lights? - waiting to accelerate away when the lights turn green? Everybody does it and it is considered more time-efficient. But is it so?
A recent study at Virginia Tech. by Ahmadi et al. conclusively shows that short separation distances at traffic lights do not save time and may serve only to increase the number of rear-end collisions. They find that the separation that cars maintain during free flow - the 2 seconds rule - is a good guide for separation distances (S meters) at traffic lights. Separations up to about 8 m do not impact on travel efficiency in a 30 mph zone.
The experimental study is described in the following three slide:
(Click on the slide to see full page image, press Escape to return to text)
We notice, for smaller separations cars in the queue take longer before start to accelerate - for example, for S = 0.38 m, the fourth car in the queue is not moving even after 6 seconds from when the first car began to accelerate (light going green). This is because a car would start to move (accelerate) only when the car in front has moved to a safe separation appropriate to a free flow driving (remember the 2-second rule).
In contrast, when S = 7.6 m, even the fifth car is able to move within the initial 6 seconds.
Notice; independent of the bumper-to-bumper distances from 0.38 m to 7.6 m, the time for all the ten cars to cross the intersection was constant to within 1 second at 23 seconds. Only for S = 15 m, where the separation is comparable to the minimum distance for comfortable driving, the time increased to 27 +- 3 second.
It would seem that keeping a larger separation in stop-go driving conditions does not impact on travel time and is much safer. Drivers should be made aware of this observation and encouraged to follow the conclusions. I might have saved my time spent in pursuing four insurance claims which thankfully settled in my favour.
The study explains these experimental observations using a theoretical model and I encourage you to visit their publication for details.
I wish to thank Professor Jonathan Boreyko (BEAM, Virginia Tech.) for his kind permission to use some of the material from the study.
Post Script: The 2-second rule gives the following safe spacing for driving at different speeds
70 mph S = 62 m; 50 mph S = 44 m; 30 mph S = 26 m and 20 mph S = 17 m.
Considering that the reaction time of the driver might be of the order of 1 second (she may be tired too), the 2 seconds rule over-estimates the recommended separations by a factor of may be two for 20 or 30 mph zones.
Who Am I? Index of Blogs.
Among all 3-D solids, for a given volume V, a sphere has the smallest surface area S.
This statement is universally made. But for me, it has been almost impossible to find a proof of this statement. Another question I have often wondered is, how different the ratio S/V is for other 3-D shapes compared to a sphere. In the following, I provide a full analysis for a cylinder, a cone, a rectangular box and a spheroid (of which the sphere is a special case). Let us first look at the sphere to set the baseline.
(Click on a slide to view its full page image, Press Escape to return to text)
Sphere: For a sphere, the situation is straightforward. The volume and the surface area of a sphere are completely determined by its radius R. This is shown in slide 1.
Cylinder: The volume and surface area of a cylinder are expressed as in slide 2.
Cone:
Rectangular Box:
In the above discussion, we have obtained general expressions for a cylinder, a cone and a rectangular box. These are very useful to obtain insight into the situation: for example, we found that minimum surface area of a cylinder happens when its height is twice its radius, or for a cone the condition is that the slant height is three times the radius of the circular base, etc.
We can, of course, use a spreadsheet (I have used EXCEL) to check the general results also and obtain a good understanding how the surface area increases with the parameter of interest.
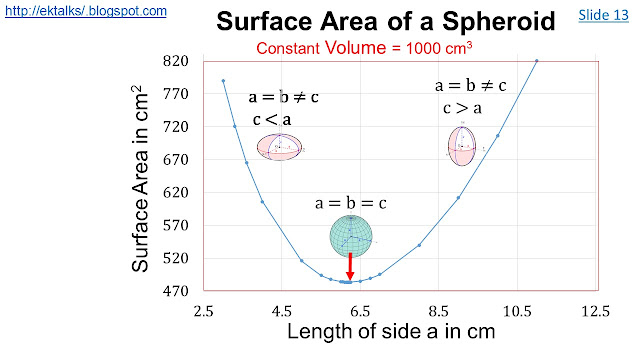
This is shown in the next 3 slides for a given volume of 1000 cm^3.
The minimum surface areas are significantly greater than for a sphere of volume 1000 cm^3 which has a surface area of 483.6 cm^2.
Spheroid: I now return back to the case of a sphere which is a special member of the ellipsoid family. An ellipsoid is a surface that may be obtained from a sphere by deforming it by means of directional scalings. The three principal axes of an ellipsoid are of unequal lengths.
In order to keep the discussion simple, we shall consider a simplified ellipsoid - a spheroid that has two of its axes equal in length. This is shown in the next three slides: (See also)
I have shown here that, for the solids considered, a sphere indeed has the smallest surface area for a given volume.
It might be interesting for you to find examples where this fact is manifested in nature and design.
Final Word: You might have noticed that for cylinders, cones and boxes, when the length parameter goes to zero or to very large values, the surface area tends to infinity. This is simply because the 3-D surface tends to approximate a 2-D plane of large dimensions.
Blogger Profile and Index of Blogs
Suppose you wish to visit a point half way up a conical mountain.
The question is -- what path would you choose?
One could use the shortest path from your base at ground level expecting to save time and energy and build the shortest road/railroads for cars/trains to travel on. But is this feasible? - Apparently not, as the slopes one would face are just too high for all forms of transport.
Ever wondered why mountain roads generally loop round? This is to manage the slope of the road that you can bicycle on, or drive a car. In this blog, I shall analyse the design considerations of a mountain road with a reasonable slope and calculate the length of the road required to visit a point half way up the mountain.
We shall learn some interesting properties of cones using geometry and school level maths.
As shown in the figure, we can 'develop' a 3-D cone into a 2-D surface -- this makes life much easier. For a right circular cone of slope length L, the 2-D shape is a segment of a circle of radius L. For ease of discussion, let us consider that the segment subtends an angle of 120 degrees at the centre of the circle.
We shall express angles in radians -
1 radian is 180/Pi degrees where Pi = 3.142.
(click on the figure to see full page image)
1. Shortest Path: This has been discussed at several places and I refer you to these(1, 2, 3, 4). The situation is really quite straight forward and is explained in the following figure:
Notice, how the path to point P (shown by the red curve) starts at a steep angle of 60 degrees from the horizontal plane (plane for the base of the cone). The path also goes uphill beyond point P and then reaches P through the downhill part.
Even if we were to take the shortest path from A to return back to A (path AB in the previous figure), it will follow the green curve with a slope of 48 degrees.
These slopes are absolutely too steep for any transport and impractical for that reason.
Let us try to understand why paths that look straight on a 2-D cone template actually are curved on the 3-D cone. This is explained in the next figure
As discussed previously, on folding the 2-D template, the circular segment BWA, becomes a closed circle and sits on a horizontal plane while radii VB, VS, VQ etc. lie on the sloping sides of the cone. Paths from A (AB and AP) make different angles with these radii as one moves away from point A.
Path AB: The path starts pointing upwards with a positive slope relative to tangent at A. The tangent lies in a horizontal plane. This angle decreases until point F where the path is parallel to the tangent at W - here the path has zero slope. Beyond point F, the path has a negative slope as shown in the figure. F is the midpoint of path AB.
Path AP: The path follows same pattern as path AB but now the path has zero slope at position G, and the portion GP has a negative slope (goes downward).
2. A Realistic Solution: To construct a path that most modes of transport may be able to use, let us first look at how slopes in roads are defined and what the maximum slopes on existing roads are.
Please Note:
https://www.theguardian.com/uk-news/2019/jul/16/street-in-wales-wins-guinness-world-record-steepest Ffordd Pen Llech in the historic town of Harlech has a gradient of 37.5% at its steepest point
Some of steepest roads in Scotland are listed here.
2. A constant Gradient Path: We shall now consider a realistic path that cars can travel and shall choose a gradient of 1 in 6 (1:6) or approximately 10 degree slope of the road. The path makes an angle of ~10 degrees (1/6 radian) with the horizontal (base of the cone) throughout the ascent. In the figure below, this is represented by the Greek letter theta (Θ) i.e. Θ = 1/6.
First we do a general analysis:
Notice that after travelling a short distance AP, the car has moved up the slope by a distance ZP = dL and the line VA has turned through an angle ε. Therefore, we can write
AP = S1= L ε and ZP = dL = L ε Θ eq. 1
The remaining length of the slope after one step ___ L1 = L - dL = L (1 - εΘ)
In the next step of angle ε,
the car will travel a shorter distance equal to (L - dL)ε and the total distance travelled in the first two steps is equal to (use eq.1)
S1 + S2 = Lε + (L - dL)ε = Lε + (L - L εΘ)ε = Lε (1 + (1 - εΘ)).
The remaining length of the slope after two steps
L2 = L1 - L1 εΘ = L1 x (1 - εΘ) = L x (1 - εΘ)^2
In the third step, the distance travelled is
S1 + S2 + S3 = Lε {1 + (1 - εΘ) + (1 - εΘ)^2}
The remaining length of the slope after three steps
L3 = L2 - L2 εΘ = L2 x (1 - εΘ) = L x (1 - εΘ)^3
and so on till a full circle of the cone is completed -
this requires N = 120/ε steps (angles expressed in degrees). We can write that the total distance travelled to complete one full circle of the cone is
S = L ε {1 + (1 - εΘ) + (1 - εΘ)^2 + ... N terms} eq.2
and the length of the slope remaining is
L(remaining) = L x (1 - εΘ)^N eq.3
The car would have climbed a distance H equal to
H = L - L(remaining) = L (1 - r^N) where r = 1 - εΘ eq.4
In eq.2, the right hand side is a geometric series with a multiplier r = (1 - εΘ)
The sum may then be written as
S = L ε (1 - r^N)/ (1-r) = H ε/(εΘ) = H /Θ eq.5
Now we are ready to calculate some numbers.
Let us say that each step is equal to a turn of 1 degree or 1 x Pi/180 = 1/57.3 radian. Therefore,
ε =1/57.3 radian; Θ = 1/6 radian and N = 120.
Equations 4 and 5 then give:
For One Loop: H = L (1 - 0.705) = 0.295 L ~ 0.3 L
S = H/(1/6) = 0.295 x 6 L = 1.77 L
The circumference of the base of the cone is L times 2Pi/3 = 2.095 L.
After one round, the car has moved up 29.5% of the slope towards the vertex of the cone and travelled a distance of 1.77 times the length of the slope.
If we continue to a second loop around the cone then an exactly the same analysis can be carried out but with the starting value of the slope length appropriate for the remaining cone. Alternately, we can use equations 4 and 5 with N = 240 to represent two loops.
For two loops (N = 240) the result will be
H = L (1 - 0.497) = 0.503 L
S = H/(1/6) = 0.503 x 6 L = 3.02 L
These results are shown in the following figure:
Some points to note here: The choice of ε equal to one degree angle is quite good. I checked by using ε = 0.1 degree and the result does not change suggesting that the calculation is secure. Also, I have chosen a slope angle of 1/6 radian (about 10 degrees) that I think is realistic. The method described above should be accurate up to a slope of about 20 degrees. For more steep slopes, it will be better to use actual trigonometric relations but that will make the analysis more complicated - and also then road gradient less practical.
Interestingly, our choice of a 1:6 gradient takes the car to the half way point in two loops. Of course, one can use equation 4 and calculate the gradient of the road required to reach a certain point on the mountain after a given number of loops.
For example, if we wish to reach the half way point in one loop, the we can use eq.4 for H = 0.5 L and find Θ (the slope required). Simple calculator work gives Θ = 0.33 radians or 18.9 degrees.
Eq.5 then tells us that the length of the path S = 1.515 L.
We can summarize the results as follows:
To reach the half way point
Shortest Path: Θ = 60 degrees, S = 1.32 L
Road with one loop: Θ = 18.9 degrees, S = 1.52 L
Road with two loops: Θ = 10 degrees, S = 3.02 L
Hope you have enjoyed reading this blog and feel more comfortable about analyzing conical structures.