Surface to Volume Ratio for a Spheroid, Cylinder, Cone and Rectangular Box - A Quantitative Analysis

Who Am I?  Index of Blogs.

Among all 3-D solids, for a given volume V, a sphere has the smallest surface area S.  

This statement is universally made. But for me, it has been almost impossible to find a proof of this statement. Another question I have often wondered is, how different the ratio S/V is for other 3-D shapes compared to a sphere.  In the following, I provide a full analysis for a cylinder, a cone, a rectangular box and a spheroid (of which the sphere is a special case). Let us first look at the sphere to set the baseline.
(Click on a slide to view its full page image, Press Escape to return to text)

Sphere:  For a sphere, the situation is straightforward.  The volume and the surface area of a sphere are completely determined by its radius R.  This is shown in slide 1.  

Cylinder:   The volume and surface area of a cylinder are expressed as in slide 2.

Cone:

 Rectangular Box:

In the above discussion, we have obtained general expressions for a cylinder, a cone and a rectangular box.  These are very useful to obtain insight into the situation: for example, we found that minimum surface area of a cylinder happens when its height is twice its radius, or for a cone the condition is that the slant height is three times the radius of the circular base, etc.
We can, of course, use a spreadsheet (I have used EXCEL) to check the general results also and obtain a good understanding how the surface area increases with the parameter of interest.  
This is shown in the next 3 slides for a given volume of 1000 cm^3.

The minimum surface areas are significantly greater than for a sphere of volume 1000 cm^3 which has a surface area of 483.6 cm^2.

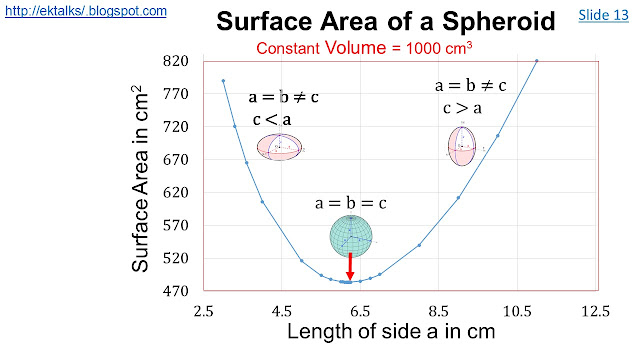
Spheroid:  I now return back to the case of a sphere which is a special member of the ellipsoid family.  An ellipsoid is a surface that may be obtained from a sphere by deforming it by means of directional scalings.  The three principal axes of an ellipsoid are of unequal lengths.      
In order to keep the discussion simple, we shall consider a simplified ellipsoid - a spheroid that has two of its axes equal in length. This is shown in the next three slides: (See also)

I have shown here that, for the solids considered, a sphere indeed has the smallest surface area for a given volume.  
It might be interesting for you to find examples where this fact is manifested in nature and design.

Final Word:  You might have noticed that for cylinders, cones and boxes, when the length parameter goes to zero or to very large values, the surface area tends to infinity.  This is simply because the 3-D surface tends to approximate a 2-D plane of large dimensions.