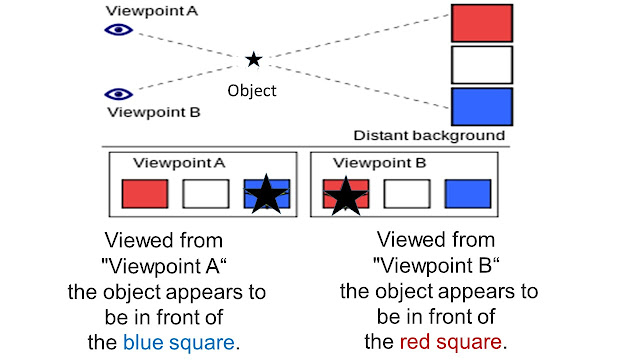
Parallax is the apparent change in position of an object relative to distant background objects resulting from a change in position of the observer.
Parallax means change and is derived from the Greek word parallaxis.
When traveling in a fast moving train, children often ask questions about the rotating landscape ; the video link demonstrates very well this example of parallax.
Schematically, the slide (adapted from Wiki) explains how parallax works:
You can observe parallax if you first view the thumb of your stretched out hand against the objects near the wall with one eye closed. Now viewing the thumb with the other eye will show a shift in its previous position against the background objects. Do try this simple demonstration yourself.
The two eyes see the thumb in different positions - actually our brain corrects for this change in apparent position as seen by the two eyes to provide one sharp image of the thumb. From this information (parallax), the brain also estimates the distance of the object from us - kind of 3-D perception already built in the processing of images we see with our eyes. Many birds and insects, do not have much overlap in the fields of view for the two eyes and tend to move their head sideways or up and down to generate depth perception. (This is called motion-parallax).
We now understand what parallax is - and that it is already useful for depth perception for humans. What else is it good for? As it turns out parallax is of fundamental importance in many fields. I shall look at two in detail here - measuring distances to stars and locating virtual images.
Distances to Stars: The first step in understanding the Universe is to measure its size - how far stars and galaxies are from the Earth. Such distances are measured through a series of methods that have overlapping validity - a cosmic distance ladder. Parallax method is the base rung of the ladder and other methods are calibrated using parallax measured distances as standard.
The distances involved are very large and require a large base line - biggest possible separation between the two points of observation. The change in viewing direction - parallax angles - also get smaller as the distance to a star increases. The biggest distance available to us is the diameter of Earth's orbit around the Sun - roughly 300 million kilometers. The average value of the radius of Earth's orbit is very nearly 150 million km and is called the Astronomical Unit (AU). The following slides explain how distances to stars are determined by the parallax method:
The parallax method defines Parallax Second or parsec or pc as a new unit of distance for astronomy.
"A star with a parallax of 1 arcsec has a distance of 1 Parsec (pc).
One parsec (pc) = 206,265 AU = 3.086 x1013 km.
Another unit of distance that is frequently used in astronomy is a Light Year (Ly). Light travels 300 million km in one second.
The distance traveled by light in a year is one light year.
A light year (Ly) = 0.31 pc = 61,270 AU = 0.96 x 1013 km.
For completeness: 1 pc = 3.26 Ly
From the slide, we notice that the distance D in pc to a star is equal to 1AU divided by the parallax p in arcsec.
The parallax angles are generally very small and difficult to measure. Temperature fluctuations in the atmosphere blur the star view and limit measurements to 0.01 arcsec or 100 pc - no more than 100 stars are in that range.
Space based telescopes Hipparcos (launched by ESA in 1989) provide a better more accurate measurement of star parallaxes down to 0.001 arcsec or distances to 1000 pc. Hipparcos has measured distances of about 100,000 stars. 1000 pc is still only a small fraction of the Milky way that is 30,000 pc across.
ESA launched Gaia in December 2013 to chart a 3-D map of the Milky Way to reveal the composition, formation and evolution of the Galaxy. Gaia is designed to measure positions of more than 200 million stars to an accuracy of 0.00001 arcsec (distances to 100,000 pc).
On 13 September 2016, Gaia has published the precise position on the sky and brightness of 1142 million stars.
Locating Virtual Images: In a somewhat less esoteric application, parallax may be used to locate virtual images formed by mirrors and concave lenses. Consider the case of a plane mirror - you see your image formed but where is it? How do you pin it down? We can do it by using parallax.
The slide shows how a virtual image is formed in a plane mirror: But where is it?
In the formation of the virtual image, rays of light from each point do not penetrate the mirror. They are reflected back to you and appear to come from a point behind the mirror. Geometrically, using the laws of reflection, it can be shown that the image is exactly the same distance behind the mirror as you are in front of it. But can we locate it?
We can locate the virtual image using parallax method. the idea is as follows:
If you view the two pins in the following slide along the line of sight shown then they will appear to overlap. But on moving the head sideways, they separate in a particular manner that helps you to decide which of the two pins is nearer to you.
Well,this is essentially what you need to do. Place a pin at the back of a plane mirror and change its position until the parallax between the pin and the virtual image is removed - they move together as one unit as you move your head sideways. The position of the pin is the position of the virtual image.
Convex mirrors and concave lenses also form virtual images. These can be located following the same method that I have describe for a plane mirror.
The parallax angles are generally very small and difficult to measure. Temperature fluctuations in the atmosphere blur the star view and limit measurements to 0.01 arcsec or 100 pc - no more than 100 stars are in that range.
Space based telescopes Hipparcos (launched by ESA in 1989) provide a better more accurate measurement of star parallaxes down to 0.001 arcsec or distances to 1000 pc. Hipparcos has measured distances of about 100,000 stars. 1000 pc is still only a small fraction of the Milky way that is 30,000 pc across.
ESA launched Gaia in December 2013 to chart a 3-D map of the Milky Way to reveal the composition, formation and evolution of the Galaxy. Gaia is designed to measure positions of more than 200 million stars to an accuracy of 0.00001 arcsec (distances to 100,000 pc).
On 13 September 2016, Gaia has published the precise position on the sky and brightness of 1142 million stars.
Locating Virtual Images: In a somewhat less esoteric application, parallax may be used to locate virtual images formed by mirrors and concave lenses. Consider the case of a plane mirror - you see your image formed but where is it? How do you pin it down? We can do it by using parallax.
The slide shows how a virtual image is formed in a plane mirror: But where is it?
In the formation of the virtual image, rays of light from each point do not penetrate the mirror. They are reflected back to you and appear to come from a point behind the mirror. Geometrically, using the laws of reflection, it can be shown that the image is exactly the same distance behind the mirror as you are in front of it. But can we locate it?
We can locate the virtual image using parallax method. the idea is as follows:
If you view the two pins in the following slide along the line of sight shown then they will appear to overlap. But on moving the head sideways, they separate in a particular manner that helps you to decide which of the two pins is nearer to you.
Convex mirrors and concave lenses also form virtual images. These can be located following the same method that I have describe for a plane mirror.






No comments:
Post a Comment